Entropy Estimation

Return to Home or Overview of Professional Activities.

Return to Research Projects list.

Last updated on 14 January 2012.

What is this about?

Information theoretic (IT) methods are now routinely used for natural sciences data analysis. For example, in neuroscience one uses IT tools to understand mechanisms by which neurons encode sensory information, while in molecular systems biology the same techniques help to uncover statistical associations among concentrations of various molecules. The strength of the methods comes from the very limited assumptions that go into them. For example, it is appealing to quantify all statistical dependencies among variables, but not just linear ones. However, the widespread use of the IT methods has been hindered by a major difficulty: it is hard to estimate entropy from experimental datasets of realistic sizes. It turns out that estimators are typically biased. For example, for estimation of entropies of discrete data, most common methods result in a bias of $\propto 2^{S}/N$, where $S$ is the (unknown) entropy and $N$ is the data set size (see this review for details). In the recent years, many methods (some described here) have been developed to solve the problem, but the majority only works when $2^{S}/N\ll 1$ (for discrete variables), or requires strong assumptions about the smoothness of the underlying probability density (for continuous variables).

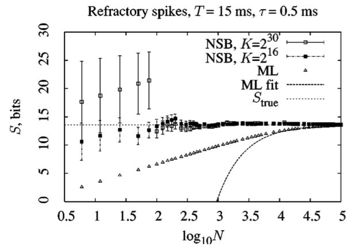
Our goal has been to solve this problem, at least under certain weak assumptions. We've made some progress. In particular, for severely undersampled data, our NSB method is probably still the most powerful, ten years after we proposed it. For example, the plot to the left show the convergence of various entropy estimators to the true entropy value when the data set size grows. The NSB method clearly converges better.

Results

NSB entropy estimator

Our NSB entropy estimator reduced the entropy estimation bias to $2^{S/2}/N\ll 1$ for a large class of data. The method doesn't work always, but it is possible to diagnose when it fails and, even in these cases, it performs not worse than most traditional estimators.

If you are interested in the NSB method, the following link will be of use:

• SourceForge-hosted project that implements the NSB method in C++ and Octave/MatLab, http://nsb-entropy.sf.net .
• Original paper that introduced the method, Nemenman et al., 2002.
• Nemenman, 2011b elucidates the coincidence-counting nature of the estimator and analyzes a lot of its technical properties.
• The following papers have applies the estimator for different natural datasets: Nemenman et al., 2004, Nemenman et al., 2008.
• You can also see some additional discussion of entropy estimation methods.

Differences of information quantities

In many cases, in particular when IT quantities are used as a measure of statistical interactions, the precise values of these quantities are less important than their rankings (i.e., the sign of their differences). In the case of mutual information, we showed in Margolin et al., 2006a that the latter task is much easier than the former, and it can be completed with almost any estimator with very little prior tuning.