Physics 380, 2011: Homework 8

Back to the main Teaching page.

Back to Physics 380, 2011: Information Processing in Biology.

1. Let's examine a human photoreceptor in detail. Come to a mirror and estimate your pupil size. Search online, http://en.wikipedia.org/wiki/Photoreceptor_cell, for the number of photoreceptors in the human retina and their size and distribution over the retina. Do these numbers make sense? That is, recall your Physics 142 and calculate the diffraction limit for resolving a point light source that emits at 500nm wavelength. How does this compare to the size of vertebrate receptors?
2. Assume that an enzyme $E$ can bind a substrate $S_{1}$ with the rate $k_{11}$. It converts it to the product $P_{1}$ with the rate $k_{21}$ or releases it back at a rate $k_{-11}$. It can also bind a substrate $S_{2}$ with the rate $k_{12}$, convert it to the product $P_{2}$ with the rate $k_{22}$ or releases it back at a rate $k_{-12}$. However, it cannot bind both substrates at the same time. Calculate the production rate of the product $P_{2}$ in this case in the quasi steady state limit.
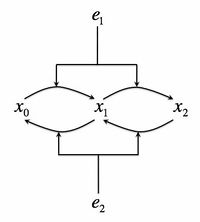
3. Consider the following biochemical signaling circuit, which is supposed to represent the Mitogen-activated protein (MAP) kinase pathway, which is one of the most universal signaling pathways in eukaryotes. A protein can be phosphorylated by a kinase, present in a concentration $e_{1}$. The kinase then must dissociate from the protein. It can then rebind it again and phosphorylate it on the second site. The total protein concentration is $x_{\rm {tot}}$ and unposphorylated, singly, and doubly poshporylated forms will be denoted as $x_{0},x_{1},x_{2}$ respectively, so that $x_{\rm {tot}}=x_{0}+x_{1}+x_{2}$. At the same time, a phosphotase with concentration $e_{2}$ is dephosphorylating the protein on both sites. See the adjacent figure for the cartoon of this signaling system.
   

   MAPK signaling cartoon
   However, for this problem we assume that production of both $x_{1}$ and $x_{2}$ just started, their concentrations are near zero, and so there is nothing yet to dephosphorylate.
   • Write a set of differential equations that describes the rate of production of $x_{1}$ and $x_{2}$.
   • Sketch the rate of production of $x_{2}$ at this initial moment as a function of $x_{\rm {tot}}$.