Stochastic dynamics on biological networks
Return to Home or Overview of Professional Activities.
Return to Research Projects list.
Last updated on 14 January 2012.
What is this about?
A single copy of a binding site on a DNA, few transcription factors, a handful of ion channels, or a small population of competing individuals all result in stochastic, counting noise --- same conditions may result in slightly different responses. Hence in a simple observation:
- Information processing in biological systems is probabilistic.
Additionally, analysis of these information processing processes gets especially complex because the networks are large, and even enumeration of states they can exist in is, essentially, impossible. In view of this, we are interested in understanding:
- Which kind of limits on the fidelity of biological information processing are imposed by its probabilistic nature? By the structural characteristics of biological networks and dynamical laws?
- Are there low-dimensional, phenomenological, coarse-grained degrees of freedom describing the networks' structure and stochastic dynamics on them that preserves the probabilistic mapping of input signals onto responses, and yet are simple, comprehensible, and relatively easy to model?
In other words:
- Can we build a general theory of stochastic biological dynamics and use it to understand the function of specific biological systems?
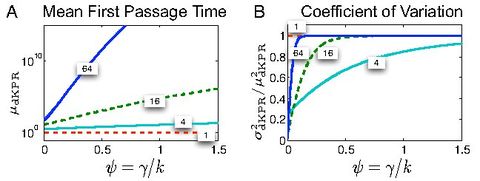
For example, the image to the left, from Bel et al., 2010 shows emergence of such low-dimensional, coarse-grained behavior (indicated by the curves reaching 1 on the second panel) in a certain type of biochemical networks, called Kinetic Proofreading Networks.
To answer these questions, we use the tools of information theory and nonequilibrium statistical mechanics. Specifically, our model systems have included various toy biochemical models, as well as NF-kB signaling, and Lotka-Volterra dynamics. Field-theoretic representations of stochastic processes (Doi-Peliti, generating functional, etc.) have previously been useful in our work on various systems.
Results
- We have discovered that the Berry phase, a staple of quantum mechanics, is also an important property of coarse-grained stochastic processes. See Sinitsyn and Nemenman, 2007, Sinitsyn and Nemenman, 2007a, Sinitsyn and Nemenman, 2010.
- We have shown that the ability of biochemical networks to process information is only weakly dependent on their topological structure. See Ziv et al., 2007, Mugler et al., 2008, Mugler et al., 2009. At the same time, many networks can be tuned to be almost optimal information processing devices.
- We have devised methods to coarse-grain biochemical signaling networks and quickly simulate them. See De Ronde et al., 2009, Sinitsyn et al., 2009.
- We have shown that a large class of biochemical kinetics networks, even with complex structure, such as Kinetic Proofreading Networks, exhibits simple large-scale functional behavior. See Bel et al., 2010, Munsky et al., 2009.
- We have shown that Berry phase and related time-dependent phenomena may have a large effect on fixation of novel mutations in evolving populations. See Otwinowski et al., 2011, Tanase-Nicola and Nemenman, 2011.
Open Problems
There are many dozens of open problems here that we still want to answer. A small sampler includes:
- What is the coarse-grained dynamics emerging in activation of many coupled receptors? Can we explain the reasons behind "spare receptors" for estrogen, T-cell receptors, and others?
- What is the effect of temporally varying fitnesses on the speed of evolution, and can prevalence of genetic recombination be explained by the variability of the environment?
- Can one develop a theory of genome dynamics in mitochondria, where selection happens on multiple levels of: mitochondrial genomes, mitochondria, and cells?
- Can certain models of diffusion in structured environments explain what seems like active transport in microscopy data?
Please email me if you want to work on this with me.