Physics 380, 2010: Information Processing in Biology

Back to Physics 380, 2010: Information Processing in Biology.

News

• The Supplementary Session times have been chosen

Logistics

• Syllabus -- we will deviate from it in the course of the class
• Supplementary instruction sections are in MSC E116, Wed 4:30-6:30, and MSC N301, Thu 5:30-7:30
• Installing Octave on your PC and Mac.

Lecture Notes

• Week 1: Physics 380, 2010: Introduction
• Week 2: Physics 380, 2010: Basic Probability Theory
• Week 3: Physics 380, 2010: Random Walks
• Week 4: Physics 380, 2010: Information Theory
• Week 5: Physics 380, 2010: Coding Theorems
• Week 6: Physics 380, 2010: Information, Gambling, and Population Biology
• Week 6: Physics 380, 2010: Fourier Analysis
• Week 7: Physics 380, 2010: Linear Response Theory

Lectures 10

• How many bits can be sent through a fluctuating molecule number?
• Gambling, population dynamics, and information theory
• Rate-distortion theory

Lecture 11, 12, 13

Fourier series and transforms

• Fourier series
• Fourier series for simple function
• Fourier transforms
• Properties of Fourier transforms
• Fourier transforms of derivatives and simple functions
• Uncertainty relation
• Power spectrum, correlation function, Wiener-Khinchin theorem
• Linear stochastic systems
• Introduction to filtering
• Frequency dependent gain
• Gain-bandwidth tradeoff
• Information in a Gaussian channel
• Fluctuation-dissipation theorem

Future Lectures

• Branching process, return in random walk process (maybe)

Homeworks

• Week 1 (due Sep 3): Introductory concepts
• Week 2 (due Sep 10): Review of Probability
• Week 3 (due Sep 17): Random Walks
• Week 4 (due Sep 24): Information Theory
• Week 5 (due Oct 1): Coding Theorems
• Week 6 (due Oct 8): Fourier series and Rate-Distrotion
• Week 7 (due Oct 15): Fourier Transforms

Weeks 8-9 (due Oct 29)

This problem is for two weeks, Oct 22 and 29, and will be due on 29th. Try to solve much of it during the first week, and I will expand the problem for the next week a bit, adding new stuff.

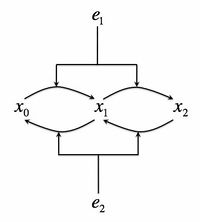
1. Consider the following biochemical signaling circuit, which is supposed to represent the Mitogen-activated protein (MAP) kinase pathway, which is one of the most universal signaling pathways in eukaryotes. A protein can be phosphorylated by a kinase, present in a concentration $e_{1}$. The kinase then must dissociate from the protein. It can then rebind it again and phosphorylate it on the second site. At the same time, a phosphotase with concentration $e_{2}$ is deposhporylating the protein on both sites. The total protein concentration is $x_{\rm {tot}}$ and unposphorylated, singly, and doubly poshporylated forms will be denoted as $x_{0},x_{1},x_{2}$ respectively, so that $x_{\rm {tot}}=x_{0}+x_{1}+x_{2}$. Let's consider the kinase concentration as the input to the circuit, $s=e_{a}(t)$ and the doubly-phosphorylated form of the protein as the output. We will consider $e_{2}$ as a constant throughout this exercise. See the adjacent figure for the cartoon of this signaling system.
   

   MAPK signaling cartoon
   • Write a set of differential equations that describes the dynamics of the species $x_{i}$. Assume that each phosphorylation/deposphorylation reaction has a Michaelis-Menten form, but be careful to realize that the same kinase/phosphotase is bound by multiple protein forms. That is, for example, the rate of phosphorylation of the protein on the first site can be written as $V_{0}sx_{0}/(1+x_{0}/K_{0}+x_{1}/K_{1})$, where $V_{0}$ is the catalytic velocity and $K_{(0,1)}$ are the Michaelis constants. Other reactions have a similar form.
   • Write equations for the steady state values of $x_{1},x_{2}$. You won't be able to solve these equations generally, and we will need to make approximations. Let's assume that all of the enzymes are working in the linear regime, so that we can drop the denominators in the Michaelis-Menten expressions.
   • Under the linear approximation above, calculate the steady state value of $x_{2}$ as a function of $e_{a}$. Plot the relation and discuss.
   • Graduate Students: Incorporate the Langevin noise into the description.
   • Now linearize the system around a steady state. That is, write $x_{i}={\bar {x_{i}}}+\Delta x_{i}$ (add noise here if a graduate student), $e_{a}={\bar {e_{a}}}+\Delta e_{a}$, and write the equations for the $\Delta x_{i}$.
   • Can we be sure that the steady state is stable? That is, will any small perturbation in $x_{1},x_{2}$ decay down to zero if given sufficient time? If not, what does it tell about the validity of our proposed analysis method?
   • Calculate the frequency-dependent gain for this system near the steady state, $g(\omega )$. Calculate its absolute value squared.
   • Plot $\left|g(\omega )\right|^{2}$ for a few different sets of parameter values, $V_{i},K_{i},e_{d},{\bar {e}}_{a}$.
   • Discuss the curves. How do they behave near $\omega =0$, near $\omega \to \infty$? Do they have peaks? Try to answer the question: What is this system's function? How do the answers to these questions depend on the choices of parameters $V_{i},K_{i},e_{d},{\bar {e}}_{a}$?
   • Grad students: On which frequencies is the noise filtered out?

This problem is related to a study in Gomez-Uribe et al. 2007. For an early, classical model the MAP kinase signaling pathway you may also see Huang and Ferrell, 1996.

Week 10 (due Nov 5)

1. In class we described bistable biochemical systems. One of the examples that we used was for a self-activating gene, which can act as a bistable, toggle switch (see articles by Gardner et al., 2000). In fact, bistability is a general example of multistability, which we have not yet described. In this problem, we will construct an example of a multistable system with three stable states.
   • Consider three genes in a network such that gene 1 strongly inhibits gene 2 and weakly inhibits gene 3; gene 2 strongly inhibits gene 3 and weakly gene 1; and gene 3 strongly inhibits gene 1 and weakly gene 2. Production should be of the Hill form, and degradation of mRNA/protein products should be linear. Do not resolve proteins from mRNA (that is, consider that a gene produces a protein directly, which later inhibits other genes).
   • Write down differential equations that would describe this dynamics.
   • Write a simple Matlab script that would solve the dynamics by the Euler method (that is, for example, $g_{1}(t+\Delta t)=g_{1}(t)+\left[P(g_{2},g_{3})-D(g_{1})\right]\Delta t$, where $P,D$ stand for production/degradation respectively.
   • Run the dynamics from different initial conditions and plot 3-d trajectories for these conditions. How many stable steady states can you find? Can you pinpoint unstable steady states this way?
   • Is the number of stable steady states dependent on the form of the gene suppression and on its strength? Elaborate by example.
2. For Grad Students (Extra credit for undergrads): Can you imagine a realistic biochemical system with just two degrees of freedom that would still have three or more stable steady states? Build such a system and complete the same analysis of it as above.

Week 11 (due Nov 12)

1. Let's discuss the effect of noise in multistable systems.
   • Take the three-gene network you designed for the previous homework. Choose the parameters so that the strongly inhibited state has 1-3 molecules, weakly inhibited has 5-10, and active state has 30-50. Make sure the system is still tri-stable.
   • Add Langevin noise to the equations describing the system.
   • Change the Matlan script from the last week to incorporate a random Langevin noise into the Euler stepping. Make sure the noise variance is correct.
   • Run the dynamics from different initial conditions and observe if the system switches randomly among the three stable states. Is there a preferential order in which these states are visited? Explain.
   • Does the distribution of switch times look like it is an exponential?
   • The following parameters work for me, but I would ask you to explore different parameter choices nearby: A=8; r=0.1; B1=10^2; B2=15^2.
2. Can this system be used as a clock?
   • Run the simulation for many switches and record the times of how long it takes the system to do one cycle through the three states, two cycles, three cycles, and so on.
   • Is the time proportional to the number of cycles? Make a plot of the number of cycles vs. the time, and see if it's linear.
   • Does the clock become better as the time grows? Explain. (Recall the Doan paper we discussed in class).

Week 12 (due Nov 19)

1. This week we are talking about noise propagation in biochemical networks..
   • Take the three-gene network you designed for the previous homework and modify it by breaking the circular dependences. That is, arrange the genes so that gene 1 is expressed at some basal level, gene 2 is suppressed by gene 1, and gene 3 is suppressed by gene 2. We will now distinguish three different maximal expression rates $A_{1,2,3}$, the degradation rates $r_{1,2,3}$, and the suppression thresholds $B_{2,3}$.
   • Set up the code so that you can simulate the system numerically (with noise) at different values of the parameters, let it settle to a steady state, and then evaluate the variance of the fluctuations around the stable steady state.

We have discussed in class that the noise in any node is given by its intrinsic noise plus the noise transferred from its parents, and the latter is multiplied by the gain and by the ratio of the response times. Let's verify this assertion.

• Let's keep all parameters fixed and vary $r_{3}$. Let's set $r_{1}>r_{2}$. Plot the coefficient of variation of gene 3 as a function of $r_{3}$ for the range of $r_{3}$ from much smaller than $r_{2}$ to much larger than $r_{1}$. Can you explain what you see on the plot?
• Now keeping $r_{3}$ fixed, and $r_{2}\gg r_{3}$, let's vary $r_{1}$ and plot the coefficient of variation of gene 3. Can you explain the plot?
• Make a similar plot of the coefficient of variation as a function of $A_{3}$. Explain what you see.
• Finally, plot the coefficient of variation as a function of $B_{2}$. Again, explain what you see.

Week 14 (due Dec 3)

This week we will work to understand adaptation in biological circuits

1. Let's try to realize circuits that would exhibit an adaptation to the mean.
   • For starters, let's consider the system similar to those that we have studied before. Let the signal $s$ activate the response $r$ by means of a Hill law with the HIll exponent of 2, and then the response is degraded with a usual linear degradation term. Let's now introduce a memory variable $m$ that is activated by the response in a similar Hill fashion and degraded (linearly) at a very slow time scale compared to the response. Finally, the memory feeds back (negatively) into the response, so that the maximum value of the response production is itself a (repressive) Hill function of the memory, but now with the Hill exponent of 1. Write a Matlab script that would take a certain signal trace on the input and produce a corresponding response for this system as the output. Do not consider the effects of noise.
   • Consider a signal that has a value of 1 for a time much longer than the inverse of either the response or the memory degradation rate, and then switches to a value of 2 and stays there for an equally long time. The response will then exhibit some initial relaxation to the steady state response. It will then jump briefly following the change in the signal, and relax close to (but not exact at) the original steady state value. Observe this in your simulations. Find the parameters of the system (the maximum production rates, the degradation rates, and the Michaelis constants) that would allow the system to be very sensitive to the changes in the input, but yet adapt almost perfectly. That is, search for the parameters such that the jump in the response following the step in the signal is many-fold (try to make it as large as possible), and yet the system relaxes back as close as possible to its pre-step steady state value.
   • You will realize that there is a tradeoff here: high sensitivity to step changes makes it hard to adapt back perfectly. It might be worthwhile reading Ma et al, 2009, where this is discussed in depth. Report the best simultaneous values of the fold-change in the response after a step in the stimulus, and the fold-change in the steady state after the relaxation and the corresponding parameters you found.
2. Now let's modify the code above to make the circuit adapt to the variance of the signal.
   • Consider a signal of a form $s=2+s_{1}\sin 2\pi t/T$, where $T,s_{1}$ are positive constants, and $T$ is such that it is much larger than the inverse of the degradation rate of the response but much smaller than the inverse of the degradation rate of the memory. Let $s_{1}$ be 1 for a long while and then switch to 2. Observe that the standard deviation of the response will jump at the transition, and then settle down, similarly to the response itself in the previous problem.
   • Let's now look for parameters that will make this response to the variance good, yet adaptive. That is, look for the largest fold-change in the response standard deviation following the step in $s_{1}$, and then for a relaxation back to (almost) the same variance as pre-step. Report the best simultaneous values you can achieve.
   • Take a look at what has changed compared to Problem 1. Hint: you probably will see that the Michaelis constant of the memory production is very different for the solutions to both of the problems, while other things don't change much. Can you explain this?

Original Literature for Presentation in Class

Working individually, or in teams of two, please select one paper from this list and be ready to present it during the identified week. I'd like you to report your selections to me by Oct 24. Selections are on First Come - First Served basis -- your first topic may be unavailable if you select late.

• Does the stochastic noise matter, and how to control it?: Week of Nov 1

1. Elowitz et al., 2002 -- this paper measures the effect of molecule noise on the single cell level
2. Blake et al., 2003 -- noise in eukaryotic transcription is investigated
3. Doan et al., 2006 -- a mechanism for noise suppression in rod cells is studies, Kohne
4. Averbeck et al., 2006 -- this paper analyzes averaging over firing of many neurons as a mean of reducing noise

• Noise propagation and amplification: Week of Nov 8

1. Schneidman et al., 1998 -- this paper discussed how channel opening and closing effects the accuracy of timing of generation of neural spike trains; Tata and Scott
2. Paulsson, 2004 -- this is a review of different phenomena that happen when stochastic noises propagate through biochemical networks
3. Pedraza and van Oudenaarden, 2005 -- a study in noise propagation in transcriptional networks, Ladik
4. Cagatay et al., 2009 -- this papers analyses the phenomenon of competence in B. subtilis to conclude that large noise if functionally important

• Adaptation and Efficient Signal encoding: Week of Nov 15

1. Brenner et al., 2000 -- this neural system is capable of changing its gain; Fountain and Yoon
2. Fairhall et al., 2001 -- this same neural system, as it turns out, is capable of adjusting its response time, A Kwon and Yu
3. Andrews et al., 2006 -- this paper analyzed the adaptation engine in E. coli chemotaxis and discusses its optimality
4. Friedlander and Brenner, 2009 -- how can an adaptive response be developed without a feedback loop?

• Performing nonlinear computations: Week of Nov 22

1. Sharpee et al, 2006 -- how do we find out which computations cell perform? are these computations optimal? Otwinowski
2. Vergassola et al, 2007 -- how can we find a source of a smell, which is a very nontrivial property of the actual smell signal we get? Um and Cho
3. Celani and Vergassola, 2010 -- this (hard) paper analyzes the computation that an E. coli must do to maximize its nutrient intake

• Learning as information processing: Week of Nov 29

1. Gallistlel et al., 2001 -- this paper argues that a foraging rat learns optimally from its environment
2. Andrews and Iglesias, 2007 -- and it turns out that an amoeba is also quite optimal, Singh

In your presentations, aim for half an hour talk. Try to structure your presentations the following way:

1. What is the question being asked?
2. What are the findings of the authors?
3. Which experimental or computational tools (whichever applicable) they use in their work?
4. What in this findings is unique to the studied biological system, and what should be general?

References

The list is far from being complete now. Stay tuned.

Textbooks

1. R Phillips, J Kondev, J Theriot. Physical Biology of the Cell (Garland Science, 2008)
   • Sizing up E. coli. PDF
2. CM Grinstead and JL Snell, Introduction to Probability.
3. W Bialek, Biophysics: Searching for Principles (2010).
   • Information theory overview is in chapters 4.1 and 4.2.
   • The question of whether biology cares about bits is reviewed in section 4.3.
4. For information about Wiener processes and diffusion, a good source is: Wiener Process article in Wikipedia.
5. The most standard textbook on information theory is: T Cover and J Thomas, Elements of Information Theory, 2nd ed (Wiley Interscience, 2006).

Sensory Ecology and Corresponding Evolutionary Adaptations

1. T Cronin, N Shashar, R Caldwell. Polarization vision and its role in biological signaling. Integrative and Comparative Biology 43(4):549-558, 2003. PDF.
2. D Stavenga, Visual acuity of fly photoreceptors in natural conditions--dependence on UV sensitizing pigment and light-controlling pupil. J Exp Biol 207 (Pt 10) pp. 1703-13, 2004. PDF.

Transcriptional regulation

1. O Berg and P von Hippel. Selection of DNA binding sites by regulatory proteins. Statistical-mechanical theory and application to operators and promoters. J Mol Biol. 193(4):723-50, 1987. PDF.
2. O Berg et al. Diffusion-driven mechanisms of protein translocation on nucleic acids. 1. Models and theory. Biochemistry 20(24):6929-48, 1981. PDF.
3. M Slutsky and L Mirny. Kinetics of protein-DNA interaction: facilitated target location in sequence-dependent potential. Biophysical J 87(6):4021-35, 2004. PDF.

Signal Processing in Vision

1. P Detwiler et al. Engineering aspects of enzymatic signal transduction: Photoreceptors in the retina. Biophys. J., 79:2801-2817, 2000. PDF.
2. A Pumir et al. Systems analysis of the single photon response in invertebrate photoreceptors. Proc Natl Acad Sci USA 105 (30) pp. 10354-9, 2008. PDF.
3. F Rieke and D Baylor. Single photon detection by rod cells of the retina. Rev Mod Phys 70, 1027-1036, 1998. PDF.
4. T Doan, A Mendez, P Detwiler, J Chen, F Rieke. Multiple phosphorylation sites confer reproducibility of the rod's single-photon responses. Science 313, 530-533, 2006. PDF.

Bacterial chemotaxis

1. J Adler. Chemotaxis in bacteria. Annu Rev Biochem 44 pp. 341-56, 1975. PDF
2. H Berg and D Brown. Chemotaxis in Escherichia coli analysed by three-dimensional tracking. Nature 239 (5374) pp. 500-4, 1972. PDF.
3. E Budrene and H Berg. Dynamics of formation of symmetrical patterns by chemotactic bacteria. Nature 376 (6535) pp. 49-53, 1995. PDF
4. E Budrene and H Berg. Complex patterns formed by motile cells of Escherichia coli. Nature 349 (6310) pp. 630-3, 1991. PDF
5. E Purcell. Life at low Reynolds number. Am J Phys 45 (1) pp. 3-11, 1977. PDF
6. H Berg. Motile behavior of bacteria. Phys Today 53 (1) pp. 24-29, 2000. PDF
7. C Rao and A Arkin. Design and diversity in bacterial chemotaxis: a comparative study in Escherichia coli and Bacillus subtilis. PLoS Biol 2 (2) pp. E49, 2004. PDF
8. C Rao et al. The three adaptation systems of Bacillus subtilis chemotaxis. Trends Microbio l16 (10) pp. 480-7, 2008. PDF.
9. A Celani and M Vergassola. Bacterial strategies for chemotaxis response. Proc Natl Acad Sci USA107, 1391-6, 2010. PDF.

Eukaryotic chemotaxis

1. J Franca-Koh et al. Navigating signaling networks: chemotaxis in Dictyostelium discoideum. Curr Opin Genet Dev 16 (4) pp. 333-8, 2006. PDF.
2. W-J Rappel et al. Establishing direction during chemotaxis in eukaryotic cells. Biophysical Journal 83 (3) pp. 1361-7, 2002. PDF.

Random walks

1. G Bel, B Munsky, and I Nemenman. The simplicity of completion time distributions for common complex biochemical processes. Physical Biology 7 016003, 2010. PDF.

Information theory

1. J Ziv and A Lempel. A Universal Algorithm for Sequential Data Compression. IEEE Trans. Inf. Thy 3 (23) 337, 1977. PDF.
2. N Tishby, F Pereira, and W Bialek. The information bottleneck method. arXiv:physics/0004057v1, 2000. PDF.

Noise in biochemistry and neuroscience

1. E Schneidman, B Freedman, and I Segev. Ion channel stochasticity may be critical in determining the reliability and precision of spike timing. Neural Comp. 10, p.1679-1704, 1998. PDF.
2. T Kepler and T Elston. Stochasticity in transcriptional regulation: Origins, consequences, and mathematical representations. Biophys J. 81, 3116-3136, 2001. PDF.
3. M Elowitz, A Levine, E Siggia & P Swain. Stochastic gene expression in a single cell. Science 207, 1183, 2002. PDF.
4. W Blake, M Kaern, C Cantor, and J Collins. Noise in eukaryotic gene expression. Nature 422, 633-637, 2003. PDF.
5. J Raser and E O’Shea. Control of stochasticity in eukaryotic gene expression. Science 304, 1811-1814, 2004. PDF.
6. J Paulsson. Summing up the noise in gene networks. Nature 427, 415, 2004. PDF, Supplement.
7. J Pedraza and A van Oudenaarden. Noise propagation in gene networks, Science 307, 1965-1969, 2005. PDF.
8. N Rosenfeld, J Young, U Alon, P Swain, M Elowitz. Gene Regulation at the Single-Cell Level. Science 307, 1962, 2005. PDF.
9. B Averbeck et al. Neural correlations, population coding and computation. Nat Rev Neurosci 7, 358-66, 2006. PDF.
10. D Gillespie. Stochastic Simulation of Chemical Kinetics. Ann Rev Phys Chem 58, 35-55, 2007. PDF.
11. T Cağatay et al. Architecture-dependent noise discriminates functionally analogous differentiation circuits. Cell 139:512-22, 2009. PDF, supplement.

Memory in noisy environments

1. T Gardner et al. Construction of a genetic toggle switch in Escherichia coli. Nature 403: 339-42, 2000. PDF
2. W Bialek. Stability and noise in biochemical switches. In Todd K. Leen, Thomas G. Dietterich, and Volker Tresp, editors, Advances in Neural Information Processing Systems 13, pages 103-109. MIT Press, 2001. PDF
3. E Aurell and K Sneppen. Epigenetics as a first exit problem. Phys Rev Lett 88, 048101, 2002. PDF.
4. E Korobkova, T Emonet, JMG Vilar, TS Shimizu, and P Cluzel. From molecular noise to behavioural variability in a single bacterium. Nature, 438:574-578, 2004. PDF.
5. Y Tu and G Grinstein. How white noise generates power-law switching in bacterial flagellar motors. Phys. Rev. Lett., 2005. PDF.

Adaptation

1. N Brenner et al. Adaptive rescaling maximizes information transmission. Neuron 26, 695-702. PDF.
2. P Cluzel, M Surette, and S Leibler. An ultrasensitive bacterial motor revealed by monitoring signaling proteins in single cells. Science, 287:1652-1655, 2000. PDF.
3. B Andrews et al. Optimal noise filtering in the chemotactic response of Escherichia coli. PLoS Comput Biol 2, e154, 2006. PDF.
4. T Sharpee et al. Adaptive filtering enhances information transmission in visual cortex. Nature 439, 936-42, 2006. PDF.
5. A Fairhall et al. Efficiency and ambiguity in an adaptive neural code. Nature 412, 787-92, 2001. PDF.
6. I Nemenman et al. Neural coding of natural stimuli: information at sub-millisecond resolution. PLoS Comput Biol 4, e1000025, 2008. PDF.
7. T Friedlander and N Brenner. Adaptive response by state-dependent inactivation. Proc Natl Acad Sci USA 106, 22558-63, 2009. PDF.
8. W Ma et al. Defining network topologies that can achieve biochemical adaptation. Cell 138, 760-73, 2009. PDF.

Robustness

1. A Eldar, D Rosin, B-Z Shilo, and N Barkai. Self-Enhanced Ligand Degradation Underlies Robustness of Morphogen Gradients. Developmental Cell, Vol. 5, 635–646, 2003. PDF.
2. T Doan, A Mendez, P Detwiler, J Chen, F Rieke. Multiple phosphorylation sites confer reproducibility of the Rod's single-photon responses. Science 313, 530-3, 2006. PDF.
3. A Lander et al. The measure of success: constraints, objectives, and tradeoffs in morphogen-mediated patterning. Cold Spring Harb Perspect Biol 1, a002022, 2009. PDF

Learning

1. CR Gallistel et al. The rat approximates an ideal detector of changes in rates of reward: implications for the law of effect. J Exp Psychol Anim Behav Process 27, 354-72, 2001. PDF.
2. CR Gallistel et al. The learning curve: implications of a quantitative analysis. Proc Natl Acad Sci USA 101, 13124-31, 2004. PDF.
3. B Andrews and P Iglesias. An information-theoretic characterization of the optimal gradient sensing response of cells. PLoS Comput Biol 3, e153, 2007. PDF.
4. M Vergassola et al. 'Infotaxis' as a strategy for searching without gradients. Nature 445, 406-9, 2007. PDF.

Eukaryotic signaling

1. C-Y Huang and J Ferrell. Ultrasensitivity in the mitogen-activated protein kinase cascade. Proc Natl Acad Sci USA 93:10078, 1996. PDF.
2. N Markevich et al. Signaling switches and bistability arising from multisite phosphorylation in protein kinase cascades. J Cell Biol 164:353-9, 2004. PDF.
3. C Gomez-Uribe, G Verghese, and L Mirny. Operating regimes of signaling cycles: statics, dynamics, and noise filtering. PLoS Comput Biol 3:e246, 2007. PDF.